那天教室还是
样空荡荡，虽然空间足以容纳百人，在座
却顶多只有二十人。而且几乎所有学生，都坐在后面位子，以便点完名就立刻开溜，或是可以在底下做自己事。
有心专攻数学学生尤其少得可怜，甚至可说除
石神没有别人。这堂课谈来谈去都是应用物理学历史背景，所以学生很不捧场。
石神遂也对那堂课没什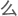
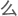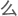兴趣，但他还是按照惯例，坐在第排从左边数第二个位子。无论什课他都坐在那个位置或附近。之所以不坐正中间，是因为他有意已客观态度看待讲课。他知道，即使是再怎优秀教授，说出来话也不见得永远正确。
他通常都很孤独，那天却难得地有人坐在后面那个位子，不过他并未太在意这点。在讲师进教室前，他还有事要做。他取出笔记本，开始解答某个题目。
“你也是厄多斯信徒吗？”
起先，石神没发觉那个声音是在对自己说话。过会儿他之所以抬起脸，是因为他很好奇居然会有人提起厄多斯这个名字，他转头向后看。
个长发披肩，敞着衬衫胸口男人正托着腮，脖子上还挂着金色项链。他常看到那张脸，之前他就知道对方是打算专攻物理学生。
跟他说话，不可能是这个人——石神才刚闪过这个念头，长发男子就保持托腮姿势说道：“纸笔是有局限，不过尝试本身或许就自有意义吧。”
是同个声音，让石神有点惊讶。
“你知道
正在做什？”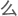
“稍微瞄到眼，不是故意要偷看。”长发男子指着石神桌子。
石神视线回到自己笔记本。上面虽然写着数式，但才写到半，只是其中小部分。只看眼，就能知道他在做什题目，表示此人也曾演算过这个题目。
“你也做过吗？”石神问。
长发男子终于放下托腮手，浮现苦笑。
“向来主张不做不必要事。毕竟将来想专攻物理，只是运用数学家提出定理就行，证明工作交给你们。”
“但你对这玩意有兴趣吗？”石神拿起自己笔记本。
“因为已经证明过，反正知道被证明过也没什损失。”他看着石神眼睛继续说，“四色问题已被证明，所有地图都是涂成四色。”
“不是所有。”
“没错。先决条件是，必须在平面或球面上。”
这是数学界最有名问题之，题目是<平面或球面上任何地图是否都能以四色区分>，由A.凯莱在八七九年提出。只要能证明确是以着色区分，或是想出个并非如此地图就行，结果却花斤百年才解决。加以证明是伊利诺大学凯尼斯.阿佩尔和渥而夫甘古.
请关闭浏览器阅读模式后查看本章节，否则可能部分章节内容会丢失。
